^{В феврале 2014 года исследователями из Калифорнии открыт новый класс многогранников. Вполне возможно, что он уже существует в природе и сможет расширить возможности архитекторов в создании новых конструктивных решений зданий и других видов искусственных сооружений.}

^{С подробными результатами их исследования можно ознакомиться в “Трудах Национальной академии наук США“.}

^{Геометрические формы привлекали к себе математиков с древних времен. Греками были описаны пять Платоновских многогранников: четырехсторонний тетраэдр, шестисторонний куб (шестигранник), восьмигранный октаэдр, 12-ти сторонний додекаэдр и 20-ти сторонний икосаэдр. Кроме этого, ими были отображены тринадцать многогранников, открытых Архимедом, включая усеченный икосаэдр, напоминающий своей формой футбольные мячи, а также прославленная молекула углерода, более известная под названием бакминстерфуллерен.}

^{Астроному и математику Иоганну Кеплеру удалось открыть третий класс — класс ромбических многогранников. Некоторые углеродные фуллерены, неорганические клетки, икосаэдрические вирусы, белковые комплексы и геодезические структуры напоминают по форме эти многогранники, которые были равносторонними, симметричными, выпуклыми и без вогнутых вмятин на поверхности.}

^{Исследователи Стэн Шейн и Джеймс Гэйд из Калифорнийского университета в Лос-Анджелесе обнаружили четвертый класс выпуклых равносторонних многогранников с многогранной симметрией. Они полагают, что природные структуры с подобной геометрией могут существовать среди вирусов и надеются, что новая геометрия фигур будет полезна для объектов, приближенных к сферической форме.}

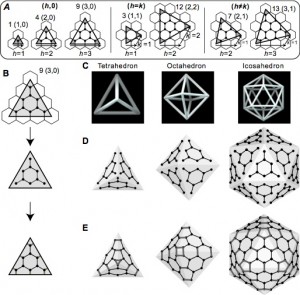
^{Построение новых фигур начинают от формы октаэдра, тетраэдра или икосаэдра. Гранями этих фигур являются равносторонние треугольники. Полученные клетки вершин и ребер часто называют Голдбергскими многогранниками. Они впервые были обнаружены в 1937 году известным математиком ХХ века Майклом Голдбергом.}

^{Повозившись с углами шестиугольников Гольдберга, Шейн и Гейд пришли к выводу, что смогут построить формы, которые будут геометрически многогранными. Более того, они будут выпуклыми, равносторонними и иметь многогранную симметрию. Они назвали открытые ими многогранники Голдбергскими.}

^{Хотя шестиугольники в этих фигурах являются равносторонними, большинство из них всё же выглядят не равносторонними и сплющенными по сравнению с правильными многоугольниками.}

^{Учёные обнаружили, что лишь один из этих многогранников создан на основе тетраэдра, другой — на базе октаэдра и бессчётное количество — на основе икосаэдра. Причём последняя форма на базе икосаэдра наиболее приближена к сферической.}

^{Предполагается, что Голдбергские многогранники могут быть использованы в природных и искусственных конструкциях, выдерживающих как внутреннее, так и внешнее давление.}